The kernel function from part 1 (shown in Figure 2.1) has a big problem (at least theoretically). It is accessing all of the required data from global memory! I've discussed (in a previous blog post) that accessing data straight from global memory is not ideal as it has long latency and low bandwidth. A common strategy is to move a subset of the data to faster (but much smaller) memory units and then repeatedly access these memory units that provide faster access and high bandwidth.

__global__ void gpu_conv2d_kernel(float const *d_N_ptr, float const *d_F_ptr, float *d_P_ptr, int const n_rows, int const n_cols)
{
    // Which output element this thread works on (Thread to output element mapping)
    int const out_col = blockIdx.x*blockDim.x + threadIdx.x;
    int const out_row = blockIdx.y*blockDim.y + threadIdx.y;
    
    // 1. Check if output element is valid
    if (out_row < n_rows && out_col < n_cols) 
    {
        // Result (in thread register)
        float p_val = 0.0f;
        
        // 2. Loop over elements of the filter array (FILTER_RADIUS is defined as a constant)
        #pragma unroll
        for (int f_row = 0; f_row < 2*FILTER_RADIUS+1; f_row++) 
        {
            for (int f_col = 0; f_col < 2*FILTER_RADIUS+1; f_col++) 
            {
                // 2a. Input element to filter element mapping
                int in_row = out_row + (f_row - FILTER_RADIUS);
                int in_col = out_col + (f_col - FILTER_RADIUS);
                        
                // 2b. Boundary check (for ghost cells)
                if (in_row >= 0 && in_row < n_rows && in_col >= 0 && in_col < n_cols)
                    p_val += d_F_ptr[f_row*(2*FILTER_RADIUS+1) + f_col] * d_N_ptr[in_row*n_cols + in_col]; // Computations
            }
        }
        // 3. Storing the final result in output matrix
        d_P_ptr[out_row*n_cols + out_col] = p_val;
    }
}

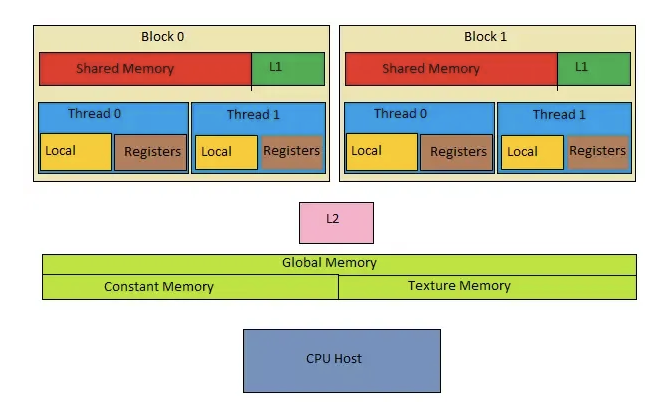
GPU Memory Units

I've previously discussed GPU memory hierarchy in detail. However, I did not cover specialized memory units like constant memory and texture memory. In this section, I will put everything together and discuss different memory units in a GPU from a programmer's point of view.

GPU is organized as an array of SMs, but programmers never interact with SMs directly. Instead, they use programming constructs like thread and thread blocks to interface with the hardware. GPU memory is divided into two parts (see Figure 2.2): off-chip and on-chip memory.

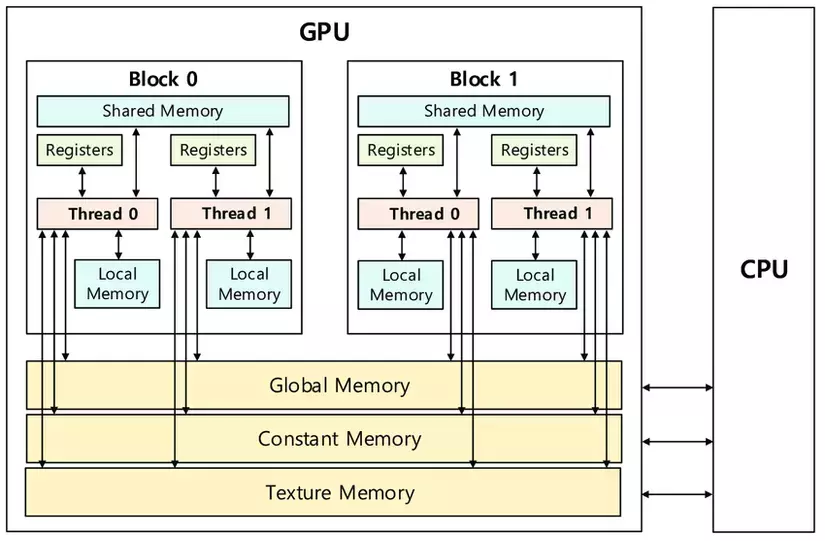
Off-chip Memory Units

1. Global memory is the largest off-chip memory unit (a few GBs).
   1. It has long latency and low bandwidth but can be accessed by all the threads in a grid.
   2. Global memory in CUDA devices is implemented using DRAM (Dynamic Random Access Memory) technology, which is quite slow compared to modern computing devices.
   3. As the DRAM access speed is relatively slow, parallelism is used to increase the rate of data access (also known as memory access throughput).
   4. This parallelism requires optimization from a programmer and is contingent on coalesced memory access. For more information, check out the section in a previous blog post: How to improve Kernel Performance?
2. Constant memory is a much smaller off-chip memory unit (~64 KB) that can be used for constant values.
   1. Constant memory is optimized for broadcast, where all threads in a warp read the same memory location.
   2. It is a faster memory unit than the global memory and can be accessed by all threads in a grid. However, the threads can't modify the contents during kernel execution (it's a read-only memory unit).
   3. For read-only memory units like constant memory, the hardware can be designed specifically in a highly efficient manner.
      1. Supporting high-throughput writes into a memory unit requires sophisticated hardware logic. As constant memory variables are constant during the kernel execution, it does not require writes, hence the manufacturer can do away with the sophisticated logic which will reduce the price and the power consumption of the overall hardware.
      2. Furthermore, constant memory is around 64 KB in size, which requires a smaller area (physically) on the board. This will, in turn, further reduce the power consumption and the price.
3. Texture memory is another specialized off-chip memory unit optimized for textures.
   1. All threads in a grid can access it.
   2. Texture memory somewhat lies in between the global and constant memory:
      1. It is smaller than global memory but larger than constant memory.
      2. Data accesses from texture memory are faster than global memory but slower than constant memory.
   3. Texture memory is optimized for 2D spatial locality, making it ideal for 2D and 3D data structures.

On-chip Memory Units

On-chip memory units reside near the cores. Hence, data access from on-chip memory is blazing fast. The issue in this case is that the size of these memory units is extremely small (maximum of ~16KB per SM). There are three main types of on-chip memory units:

1. Shared Memory
   1. Shared memory is a small memory space (~16KB per SM) that resides on-chip and has a short latency with high bandwidth.
   2. On a software level, it can only be written and read by the threads within a block.
2. Registers
   1. Registers are extremely small (~8KB per SM) and extremely fast memory units that reside on-chip.
   2. On a software level, it can be written and read by an individual thread (i.e., private to each thread).
3. Local Memory 
   1. It is local to each thread and is (mostly) used to store temporary variables.
   2. It has the smallest scope and is dedicated to each individual thread.

Constant Memory

Figure 2.1 shows that I'm accessing the filter matrix and the input image matrix from the global memory. One thing to keep in mind is that input images are high resolution (i.e., \(\approx 2000 \times 2000 \)), while the filter matrix is much much smaller (mostly \( 3 \times 3\) or \( 5 \times 5\) or \( 7 \times 7\)). I can use constant memory for the filter array because:

1. It is small in size and can easily fit in the constant memory.
2. It does not change during the execution of the kernel, i.e., I only need to read the values.
3. All threads access the filter elements in the same order (starting from F[0][0] and moving by one element at a time), and constant memory is optimized for such accesses.

To use constant memory, the host cost must allocate and copy constant memory variables in a way different than the global memory variables.

// Compile-time constant
#define FILTER_RADIUS 2

// Allocate constant memory
__constant__ float F[2*FILTER_RADIUS+1][2*FILTER_RADIUS+1];

// Move data from host memory to constant memory (Destination, Source, Size)
cudaMemcpyToSymbol(F, F_h, (2*FILTER_RADIUS+1)*(2*FILTER_RADIUS+1)*sizeof(float));

Kernel function accesses constant memory variables like global variables, i.e., I do not need to pass them as arguments to the kernel. Figure 2.3 shows the revised version that assumes a filter d_F in the constant memory.

#define FILTER_RADIUS 1
extern __constant__ float d_F[(2*FILTER_RADIUS+1)*(2*FILTER_RADIUS+1)];

__global__ void gpu_conv2d_constMem_kernel(float const *d_N_ptr, float *d_P_ptr, int const n_rows, int const n_cols)
{
    // Which output element does this thread work on
    int const out_col = blockIdx.x*blockDim.x + threadIdx.x;
    int const out_row = blockIdx.y*blockDim.y + threadIdx.y;
    
    // Check if output element is valid
    if (out_row < n_rows && out_col < n_cols) 
    {
        // Result (in thread register)
        float p_val = 0.0f;
        
        // Loop over elements of the filter array
        #pragma unroll
        for (int f_row = 0; f_row < 2*FILTER_RADIUS+1; f_row++) 
        {
            for (int f_col = 0; f_col < 2*FILTER_RADIUS+1; f_col++) 
            {
                // Input element to filter element mapping
                int in_row = out_row + (f_row - FILTER_RADIUS);
                int in_col = out_col + (f_col - FILTER_RADIUS);
                        
                // Boundary Check
                if (in_row >= 0 && in_row < n_rows && in_col >= 0 && in_col < n_cols) 
                    p_val += d_F[f_row*(2*FILTER_RADIUS+1) + f_col] * d_N_ptr[in_row*n_cols + in_col];
            }
        }
        d_P_ptr[out_row*n_cols + out_col] = p_val;
    }
}

Tiled Convolution using Shared Memory

Now that the filter matrix is handled let's focus on reducing global memory access for the input image. The strategy here is to partition the output image into multiple tiles (output tiles) and assign each to a unique block. Figure 2.4 shows that a larger input tile (blue) is required to compute an output tile (green). This complicates things, but one way to solve this problem is by keeping the block dimension equal to the input tile dimension. This will result in a simpler data transfer from global to shared memory, but the final computation of the output tile will be complicated.

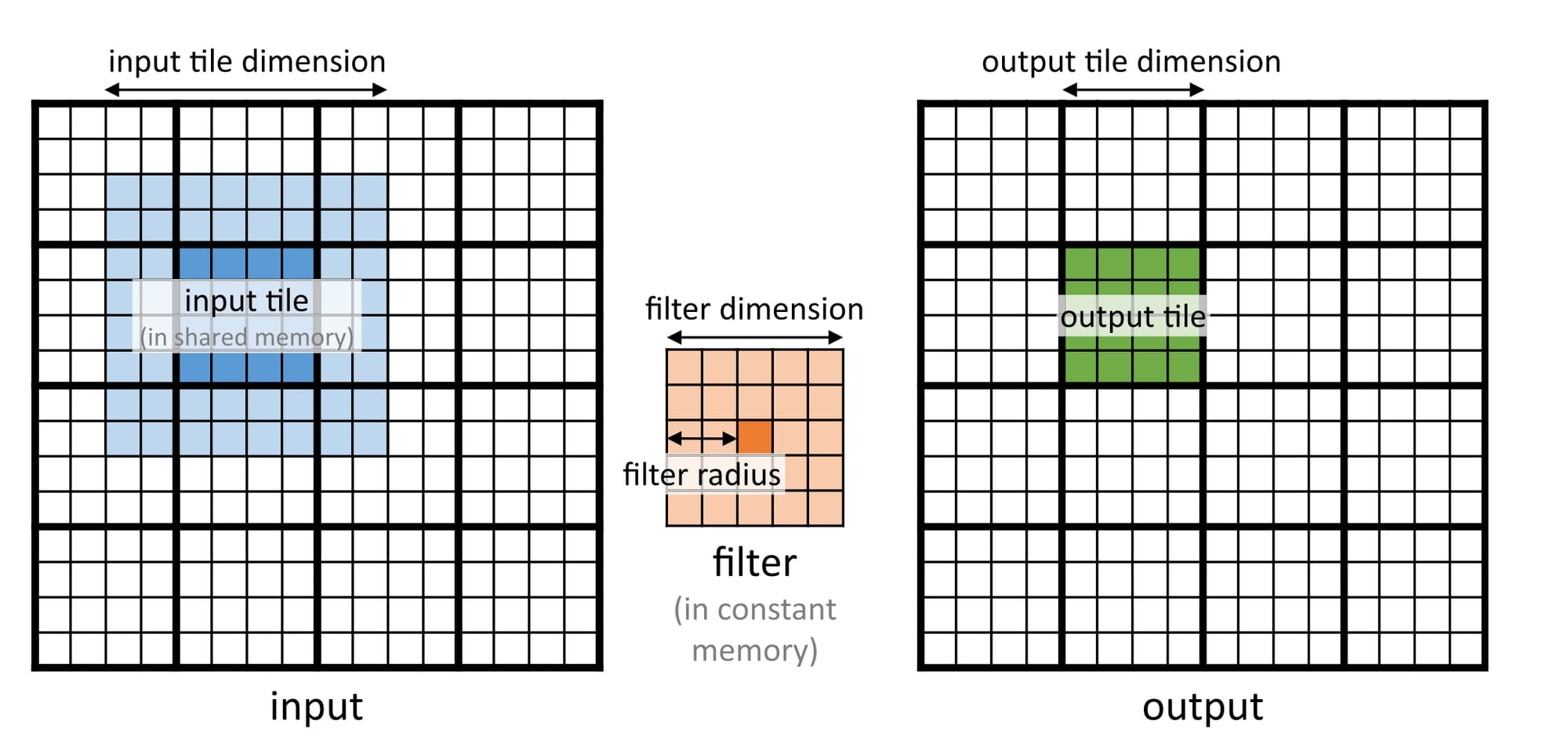
Consider an example where the input and output are \(16 \times 16\) and the filter is \(5 \times 5\). I use a block to compute a \(4 \times 4\) output tile. Remember that to compute this \(4 \times 4\) output tile, I will need an \(8 \times 8\) input tile. So, the block dimension will be \(8 \times 8\) with a \(4 \times 4\) grid (to cover all the output elements). Figure 2.5 shows the thread-to-element mapping for both input and output tiles. Notice how it naturally aligns with the input tile elements, but some of the threads lie outside the range for the output tile. I must disable these while computing the final answer.

I can write the kernel function in __ steps:

1. The kernel function starts with mapping the threads to output elements. Remember that the thread block is shifted relative to the output tile (Figure 2.5).
2. Next, shared memory is allocated.
   1. Once allocated, the input tile is copied into this shared memory. Copying the data is pretty straightforward, except I need to check for ghost cells (see Figure 2.6).
   2. Barrier synchronization must be used to ensure that the complete input tile has been loaded.

3. Once the shared memory is populated, I can proceed to the computations.
   1. The first check ensures that threads lie within the output image bounds (output ghost elements).
   2. The second check ensures that the threads lie within the output tile bounds.
   3. After all the checks, the code loops over the filter elements.
   4. Inside this loop, the mapping to the elements in the shared memory is defined, and computations are performed.
4. Finally, the results are stored back in the output array.

Figure 2.7 shows the complete code.

#define FILTER_RADIUS 1
#define INPUT_TILE_DIM 16
#define OUTPUT_TILE_DIM (INPUT_TILE_DIM - 2*FILTER_RADIUS)

extern __constant__ float d_F[(2*FILTER_RADIUS+1)*(2*FILTER_RADIUS+1)];

__global__ void gpu_conv2d_tiled_kernel(float *d_N_ptr, float *d_P_ptr, int n_rows, int n_cols)
{
    // 1. Which output element does this thread works on
    int out_col = blockIdx.x*OUTPUT_TILE_DIM + threadIdx.x - FILTER_RADIUS;
    int out_row = blockIdx.y*OUTPUT_TILE_DIM + threadIdx.y - FILTER_RADIUS;

    // 2. Allocate shared memory
    __shared__ float N_sh[INPUT_TILE_DIM][INPUT_TILE_DIM];

    // 2a. Checking for ghost cells and loading tiles into shared memory
    if (out_row >= 0 && out_row < n_rows && out_col >= 0 && out_col < n_cols)
        N_sh[threadIdx.y][threadIdx.x] = d_N_ptr[out_row*n_cols + out_col];
    else
        N_sh[threadIdx.y][threadIdx.x] = 0.0f;
    
    // 2b. Ensure all elements are loaded
    __syncthreads();

    // 3. Computing output elements
    int tile_col = threadIdx.x - FILTER_RADIUS;
    int tile_row = threadIdx.y - FILTER_RADIUS;
    
    // 3a. Check if the output element is valid
    if (out_row >= 0 && out_row < n_rows && out_col >= 0 && out_col < n_cols) 
    {
        // 3b. Checking for threads outside the tile bounds
        if (tile_row >= 0 && tile_row < OUTPUT_TILE_DIM && tile_col >= 0 && tile_col < OUTPUT_TILE_DIM) 
        {
            // Result (in thread register)
            float p_val = 0.0f;
            
            // 3c. Loop over elements of the filter array
            #pragma unroll
            for (int f_row = 0; f_row < 2*FILTER_RADIUS+1; f_row++) 
            {
                for (int f_col = 0; f_col < 2*FILTER_RADIUS+1; f_col++) 
                {
                    // 3d. Input element (in shared memory) to filter element mapping
                    int in_row = tile_row + f_row;
                    int in_col = tile_col + f_col;
                
                    p_val += d_F[f_row*(2*FILTER_RADIUS+1) + f_col] * N_sh[in_row][in_col];
                }
            }

            // 4. Storing the final result
            d_P_ptr[out_row*n_cols + out_col] = p_val;
        }
    }
}

Benchmarking

The table below compares application runtime for different versions of 2D convolution for an image of size \(2048 \times 2048\) and a \(3 \times 3\) filter:

This is unexpected. There is almost no improvement when using constant memory or tiling!

Conclusion

Using constant and shared memory (via tiling) are two very important concepts in GPU programming (even though it didn't improve things practically). However, I don't want to leave this without any analysis. The next blog post is all about analyzing why I couldn't improve the performance using constant and shared memory, and if there is anything else that I can do to reduce the application runtime.

References

1. Kirk, David B., and W. Hwu Wen-Mei. Programming massively parallel processors: a hands-on approach. Morgan kaufmann, 2016.
2. Ansorge, Richard. Programming in parallel with CUDA: a practical guide. Cambridge University Press, 2022.
3. Memory types in GPU by CisMine Ng.
4. GPU memory Coalescing
5. GPU Shared Memory