By Tushar Gautam in GPU Programming — Nov 28, 2024

Step 3: GPU Shared Memory

Tiled matrix multiplication using GPU shared memory.

Figure 1 shows the performance of the kernel with coalesced memory accesses against cuBLAS SGEMM. For 128 x 128 matrices, the performance is very close. As the matrix size increases, the gap between cuBLAS and our code increases drastically.

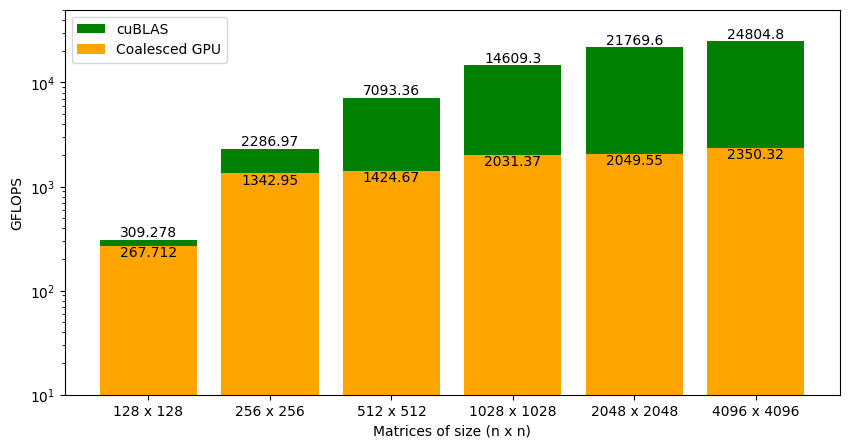
The main difference between matrix multiplication involving 128 x 128 matrices and 4096 x 4096 matrices is the amount of data accessed from global memory. As the global memory has long latency and low bandwidth, we need to find a way to reduce global memory accesses or in other words, perform more operations per byte of data accessed from global memory. To do this, we need more deeper understanding of the GPU memory hierarchy.

GPU Memory Hierarchy

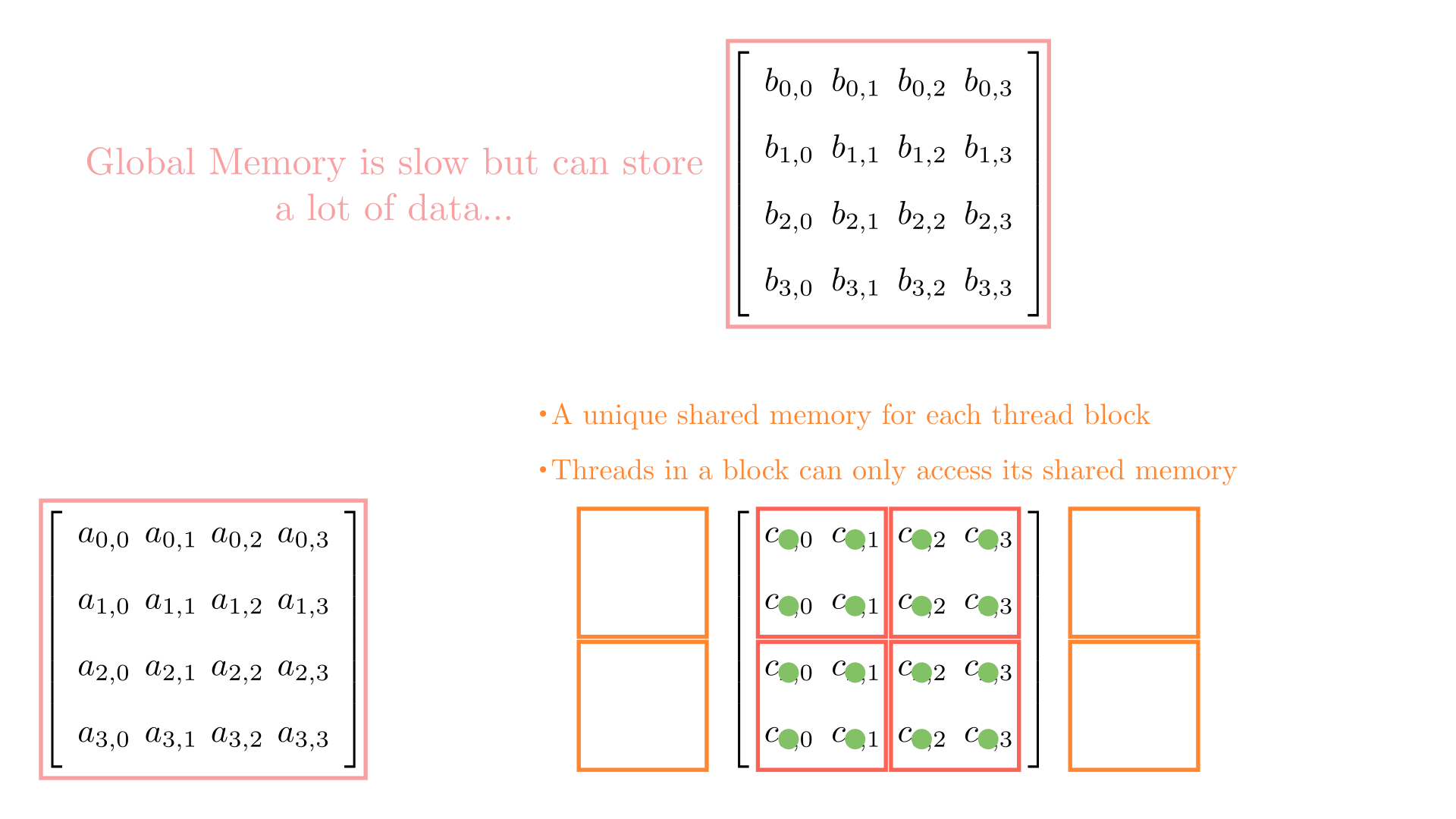
We already know that GPU is organized as an array of SMs. Programmers never interact with SMs directly. Instead, they use programming constructs like thread and thread blocks to interface with the actual hardware. When multiple blocks are assigned to an SM, the on-chip memory is divided amongst these blocks hierarchically (see Figure 2). Let's now look at the on-chip memory in more detail.

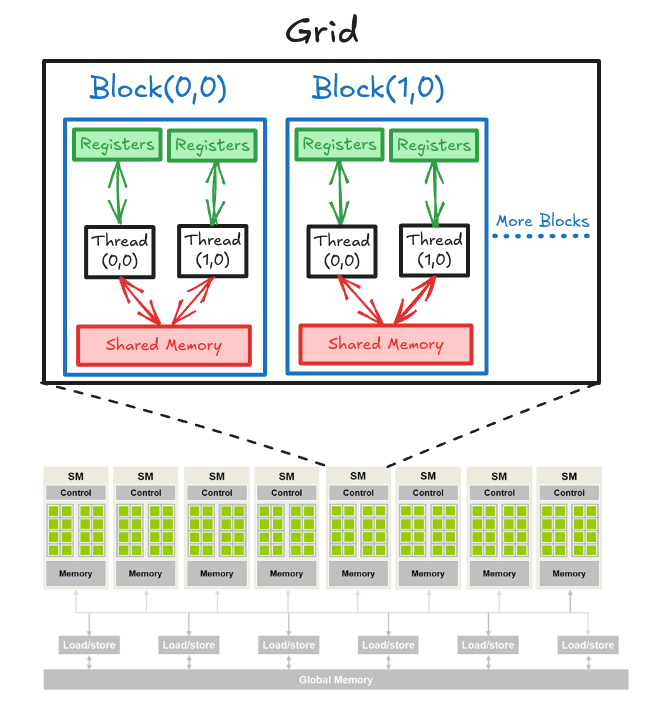
On-chip memory units reside near the cores. Hence, data accesses from on-chip memory is blazing fast. The issue in this case is that the size of these memory units is very small (maximum of ~16KB per SM). There are two main types of on-chip memory units that we can manage with code.

Shared Memory

Shared memory is a small memory space (~16KB per SM) that resides on-chip and has a short latency with high bandwidth. On a software level, it can only be written and read by the threads within a block.

Registers

Registers are extremely small (~8KB per SM) and extremely fast memory units that reside on-chip. On a software level, it can be written and read by an individual thread (i.e., private to each thread).

💡

This is in stark contrast to global memory that all threads can access!

To avoid multiple global memory accesses, we can partition the data into subsets called tiles so each tile fits into the shared memory and then perform multiple operations on this data. As accessing data from shared memory is fast, this should give a substantial speed up. However, there are two things that we need to keep in mind:

Shared memory is small, so we can only move very small subsets of data to and from shared memory (one at a time).
The correctness of the algorithm should not be affected by this strategy.

Tiled Matrix Multiplication

For simplicity, consider a matrix multiplication involving matrices of size 4. To facilitate parallel computations, let's define a 2 x 2 grid (i.e., 2 blocks each in x and y) and 2 x 2 blocks (i.e., 2 threads each in x and y). Figure 3 shows the computations involving all the blocks in the grid.

Figure 3: 4x4 matrix multiplication involving 2x2 blocks and 2x2 grid.

Let's see how each thread in this block accesses data from the global memory. As a quick recap, the for loop in the kernel function accesses the elements of A and B, one by one.

for (int k = 0; k < A_n_cols; k++)
{
    value += d_A_ptr[row*A_n_cols + k] * d_B_ptr[k*C_n_cols + col];
}

Figure 4 shows the elements accesses by each thread for values of k ranging from 0 to 2.

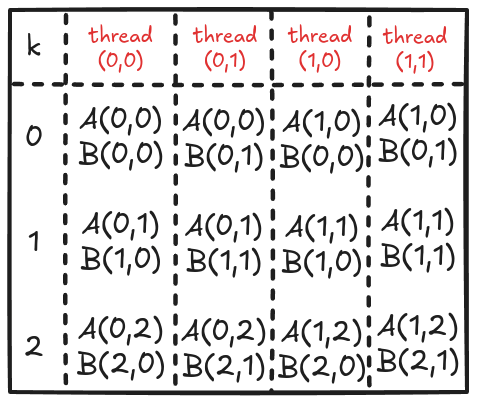
Figure 4: Threads and global memory accesses.

Analyzing these memory accesses, we see they are quite inefficient! Just look at k=0; Thread(0,0) and Thread(0,1) both access the same element A(0,0) from global memory. The same can be said for Thread(0,0) and Thread(1,0), where these two are again accessing B[0,0] individually from the global memory. These multiple global memory accesses are costly, and it would be better if we access these elements once, store them in shared memory, and then all threads in a block can use them whenever necessary!

The strategy here is to divide the matrices A and B into tiles of the shape same as that of the thread block. This is just to keep code simple. Then an outer loop (say phase) loops over the tiles (one by one). Inside each phase, each thread in the block loads one element from global to shared memory. Once all the elements are loaded in the shared memory, an inner loop (say k_phase) performs the dot product (just like k in the last kernel function). The catch here is that, all elements accessed by k_phase are in shared memory so there's very little cost associated with these memory accesses.

For 4x4 matrices, we will have two phases, and Figure 5 shows the loading of tiles into shared memory in each of those phases. One element is assigned to each thread and all threads in a block load these elements together into shared memory (in parallel). Once the elements are in the shared memory, matrix multiplication is performed using the data in the shared memory. With each iteration, the result gets accumulated and at the end have the final result that can be stored back in the output matrix.

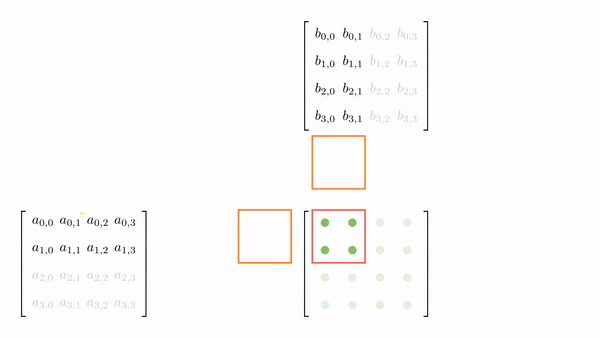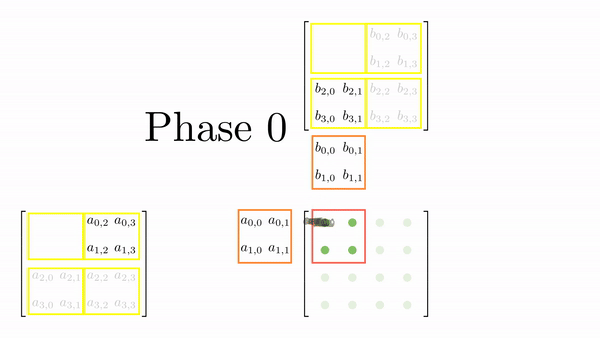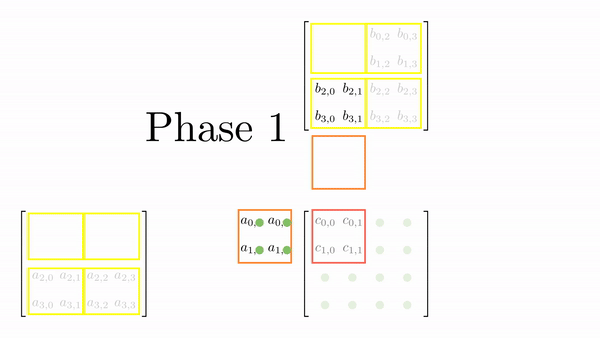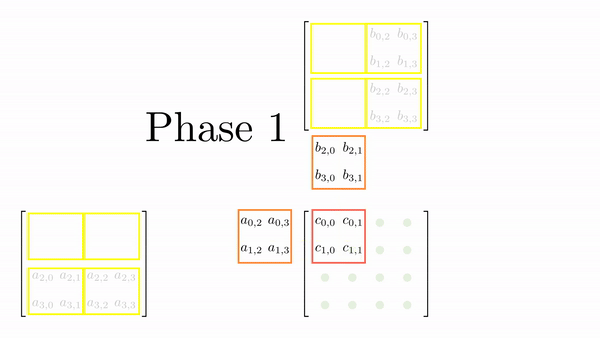
Figure 5: Loading tiles into shared memory and performing matrix multiplication in multiple phases

Figure 6 shows the elements accesses by each thread for different values of phase (keeping the data in Figure 6 consistent with Figure 4).

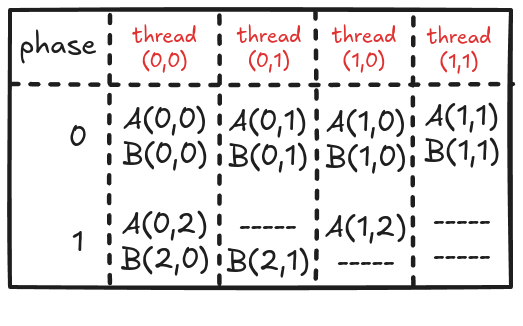
Figure 6: Threads and global memory accesses using shared memory

Each thread previously was accessing 6 elements from global memory. Now that has been reduced to 4 or 3 (almost halved). This might not look significant, but remember that we will use this code to perform large matrix multiplications (and not 4x4). It is worth noting that if the tile size is kxk (in the case discusses above, it was 2x2), the global memory traffic will be reduced to 1/k. So, the focus should be to keep the tile size as large as possible (ensuring that it fits in the limited shared memory).

The tiling works because the matrix multiplication algorithm supports it! Algorithmically, we are just splitting one large loop (k) into two smaller loops(phase and k_phase). For example, consider the calculations for computing the output element C[0,0]:

Original Version

$$C[0,0]= \overbrace{A[0,0] \cdot B[0,0]}^{k=0} + \overbrace{A[0,1] \cdot B[1,0]}^{k=1} + \overbrace{A[0,2] \cdot B[2,0]}^{k=2} + \overbrace{A[0,3] \cdot B[3,0]}^{k=3}$$

Tiled Version

$$C[0,0]= \overbrace{\overbrace{A[0,0] \cdot B[0,0]}^{k_{phase}=0} + \overbrace{A[0,1] \cdot B[1,0]}^{k_{phase}=1}}^{phase=0} + \overbrace{\overbrace{A[0,2] \cdot B[2,0]}^{k_{phase}=0} + \overbrace{A[0,3] \cdot B[3,0]}^{k_{phase}=1}}^{phase=1}$$

Writing a kernel function that supports tiling can be a little tricky. However, I will explain everything by dividing the whole process into 8 simple steps:

The very first thing we need to do is make sure that the dimensions of the block are the same as the tile size. This is just to keep the code simple.

// Ensure that TILE_WIDTH = BLOCK_SIZE
assert(TILE_WIDTH == blockDim.x);
assert(TILE_WIDTH == blockDim.y);

Let's store the block and thread indices in variables and find out the coordinate of the element of C that the select thread will work on. Then, we can also allocate shared memory for tiles of matrices A and B.

💡

Remember that automatic variables are private to threads (hence a separate copy for each thread).

// Details regarding this thread
const int by = blockIdx.y;
const int bx = blockIdx.x; 

const int ty = threadIdx.y;
const int tx = threadIdx.x; 

// Working on C[row,col]
const int row = TILE_WIDTH*by + ty;
const int col = TILE_WIDTH*bx + tx;

// Allocating shared memory
__shared__ float sh_A[TILE_WIDTH][TILE_WIDTH];
__shared__ float sh_B[TILE_WIDTH][TILE_WIDTH];

Next, we divide matrices A and B into multiple tiles (or phases) and loop over the tiles one by one.

// Phases
const int phases = ceil((float)A_n_cols/TILE_WIDTH);

// Parallel mat mul
float value = 0;
for (int phase = 0; phase < phases; phase++)
{
    // .
    // .
    // .
}

As the block size is the same as the tile width, each thread is responsible for copying an element from matrices A and B. The Figure 5 illustrates which thread will copy which element, but here are the key points:
1. For an element of matrix A, the row index is the same as the global index of the thread in the y direction (i.e., row), and the column index is decoded by first deciding which tile number it is (i.e. phase*TILE_WIDTH), and then the local thread index in the x direction (i.e. tx) is added to it (remember that the x index of the thread maps to the columns of A).
2. For an element of matrix B, the row index is decoded by first deciding which tile number it is (i.e. phase*TILE_WIDTH), and then the local thread index in the y direction (i.e. ty) is added to it (remember that the y index of the thread maps to the rows of B), and the column index is the same as the global index of the thread in the x direction (i.e., col).
3. One thing to remember is that if a thread does not load a value into shared memory, then that spot in the shared memory must be set to 0 to avoid corruption of the final results.

// Parallel mat mul
float value = 0;
for (int phase = 0; phase < phases; phase++)
{
    // Load Tiles into shared memory
    if ((row < C_n_rows) && ((phase*TILE_WIDTH+tx) < A_n_cols))
      sh_A[ty][tx] = d_A_ptr[(row)*A_n_cols + (phase*TILE_WIDTH+tx)];
    else
      sh_A[ty][tx] = 0.0f;

    if (((phase*TILE_WIDTH + ty) < A_n_cols) && (col < C_n_cols))
      sh_B[ty][tx] = d_B_ptr[(phase*TILE_WIDTH + ty)*C_n_cols + (col)];
    else
      sh_B[ty][tx] = 0.0f;
    
    // .
    // .
    // .
}

The whole point of tiling is that all threads in a block can access all elements (necessary) for their computations. As data copying into shared memory is done in parallel by multiple threads (and it's coalesced), we must ensure the complete tile is loaded before moving forward! This is done using __syncthreads() which basically holds the code execution (at this point) until all threads have reached there.

// Parallel mat mul
float value = 0;
for (int phase = 0; phase < phases; phase++)
{
    // Load Tiles into shared memory
    if ((row < C_n_rows) && ((phase*TILE_WIDTH+tx) < A_n_cols))
      sh_A[ty][tx] = d_A_ptr[(row)*A_n_cols + (phase*TILE_WIDTH+tx)];
    else
      sh_A[ty][tx] = 0.0f;

    if (((phase*TILE_WIDTH + ty) < A_n_cols) && (col < C_n_cols))
      sh_B[ty][tx] = d_B_ptr[(phase*TILE_WIDTH + ty)*C_n_cols + (col)];
    else
      sh_B[ty][tx] = 0.0f;
    
    // Wait for all threads to load elements
    __syncthreads();

    // .
    // .
    // .
}

Finally, we can perform the dot product using the data loaded into the shared memory.

// Parallel mat mul
float value = 0;
for (int phase = 0; phase < phases; phase++)
{
    // Load Tiles into shared memory
    if ((row < C_n_rows) && ((phase*TILE_WIDTH+tx) < A_n_cols))
      sh_A[ty][tx] = d_A_ptr[(row)*A_n_cols + (phase*TILE_WIDTH+tx)];
    else
      sh_A[ty][tx] = 0.0f;

    if (((phase*TILE_WIDTH + ty) < A_n_cols) && (col < C_n_cols))
      sh_B[ty][tx] = d_B_ptr[(phase*TILE_WIDTH + ty)*C_n_cols + (col)];
    else
      sh_B[ty][tx] = 0.0f;
    __syncthreads();

    // Dot product
    for (int k_phase = 0; k_phase < TILE_WIDTH; k_phase++)
        value += sh_A[ty][k_phase] * sh_B[k_phase][tx];
    
    // .
    // .
    // .
}

As the loop moves to the next iteration, it starts by loading the shared memory with new tiles. For this reason, we must again ensure that all threads have completed their dot product evaluation and avoid data corruption!

// Parallel mat mul
float value = 0;
for (int phase = 0; phase < phases; phase++)
{
    // Load Tiles into shared memory
    if ((row < C_n_rows) && ((phase*TILE_WIDTH+tx) < A_n_cols))
      sh_A[ty][tx] = d_A_ptr[(row)*A_n_cols + (phase*TILE_WIDTH+tx)];
    else
      sh_A[ty][tx] = 0.0f;

    if (((phase*TILE_WIDTH + ty) < A_n_cols) && (col < C_n_cols))
      sh_B[ty][tx] = d_B_ptr[(phase*TILE_WIDTH + ty)*C_n_cols + (col)];
    else
      sh_B[ty][tx] = 0.0f;
    __syncthreads();

    // Dot product
    for (int k_phase = 0; k_phase < TILE_WIDTH; k_phase++)
        value += sh_A[ty][k_phase] * sh_B[k_phase][tx];
    
    // Wait for all threads to finish dot product
    __syncthreads();
}

💡

You might be thinking, how can this tiled version be better because there are two loops? If you look carefully, the two loops are significantly smaller than the one big loop in the standard matrix multiplication kernel. Essentially, we are breaking a single long-running loop into smaller phases (that run faster). This technique is known as strip mining and is not unique to GPU programming.

The last step is to store the calculated value in matrix C. Again, we must ensure that the threads put back the results in the valid memory locations.

// Assigning calculated value
if ((row < C_n_rows) && (col < C_n_cols))
    d_C_ptr[(row)*C_n_cols + (col)] =  1*value + 0*d_C_ptr[(row)*C_n_cols + (col)];

Putting all 8 steps together, we have a parallel implementation of tiled matrix multiplication.

__global__ void tiled_mat_mul_kernel(float *d_A_ptr, float *d_B_ptr, float *d_C_ptr, int C_n_rows, int C_n_cols, int A_n_cols)
{
    // Ensure that TILE_WIDTH = BLOCK_SIZE
    assert(TILE_WIDTH == blockDim.x);
    assert(TILE_WIDTH == blockDim.y);
    
    // Details regarding this thread
    const int by = blockIdx.y;
    const int bx = blockIdx.x; 

    const int ty = threadIdx.y;
    const int tx = threadIdx.x; 

    // Working on C[row,col]
    const int row = TILE_WIDTH*by + ty;
    const int col = TILE_WIDTH*bx + tx;

    // Allocating shared memory
    __shared__ float sh_A[TILE_WIDTH][TILE_WIDTH];
    __shared__ float sh_B[TILE_WIDTH][TILE_WIDTH];

    // Phases
    const int phases = ceil((float)A_n_cols/TILE_WIDTH);

    // Parallel mat mul
    float value = 0;
    for (int phase = 0; phase < phases; phase++)
    {
        // Load Tiles into shared memory
        if ((row < C_n_rows) && ((phase*TILE_WIDTH+tx) < A_n_cols))
          sh_A[ty][tx] = d_A_ptr[(row)*A_n_cols + (phase*TILE_WIDTH+tx)];
        else
          sh_A[ty][tx] = 0.0f;

        if (((phase*TILE_WIDTH + ty) < A_n_cols) && (col < C_n_cols))
          sh_B[ty][tx] = d_B_ptr[(phase*TILE_WIDTH + ty)*C_n_cols + (col)];
        else
          sh_B[ty][tx] = 0.0f;
        __syncthreads();

        // Dot product
        for (int k_phase = 0; k_phase < TILE_WIDTH; k_phase++)
            value += sh_A[ty][k_phase] * sh_B[k_phase][tx];
        __syncthreads();
    }
    // Assigning calculated value
    if ((row < C_n_rows) && (col < C_n_cols))
        d_C_ptr[(row)*C_n_cols + (col)] =  1*value + 0*d_C_ptr[(row)*C_n_cols + (col)];
}

Benchmark

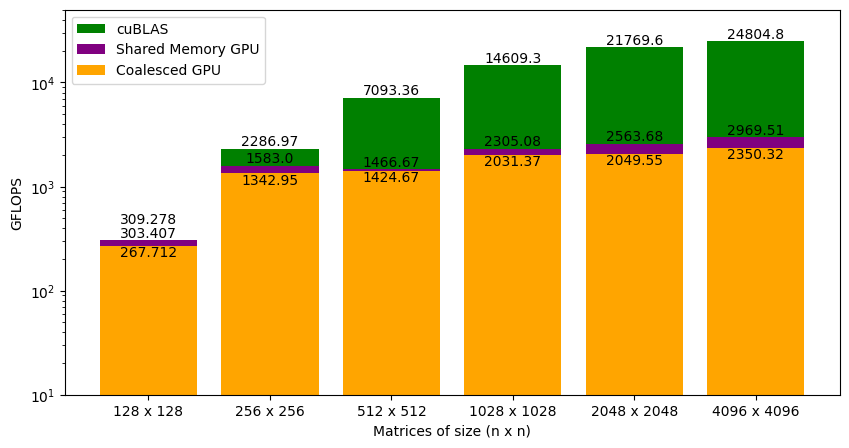
Figure 7: cuBLAS vs Coaleased vs Shared Memory

Figure 7 shows the GFLOPS for the coalesced and shared memory code (where tile size is set to 32x32) against NVIDIA's SGEMM implementation. As we saw earlier that the coalesced version was achieving around 9% of what cuBLAS can do for large matrices. With shared memory accesses, the kernel is at around 12% of cuBLAS. This did not result in a big performance jump. Again, the GFLOPS trend is similar to the coalesced version of kernel function. Our code is almost on level with cuBLAS for smaller matrices (i.e. 128 x 128), but the gap widens as the matrix size increases. We will have to analyze this further to understand why this is happening.

References

Tiled matrix multiplication on a GPU

Benchmarking tiled matrix multiplication on a GPU

GPU Memory Hierarchy

Tiled Matrix Multiplication

Benchmark

References

Subscribe to 0Mean1Sigma